Introduction aux arbres.

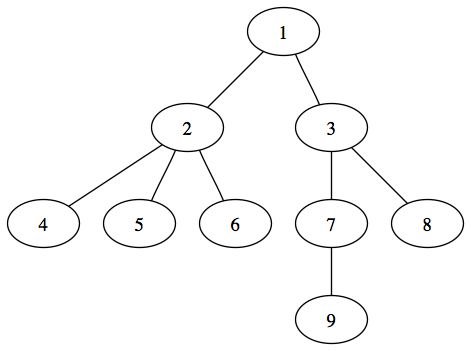
On distingue deux grands types d'arbres : les arbres enracinés et les arbres non enracinés. Le premier type d'arbre est celui qui nous intéressera le plus. Un arbre enraciné est un arbre hiérarchique dans lequel on peut établir des niveaux. Il ressemblera plus à un arbre généalogique tel qu'on le conçoit couramment. Voici un exemple d'arbre enraciné :

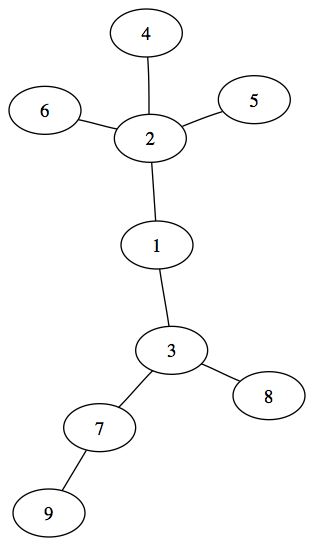
Le deuxième grand type d'arbre est un arbre non enraciné. Il n'y a pas de relation d'ordre ou de hiérarchie entre les éléments qui composent l'arbre. On peut passer d'un arbre non enraciné à un arbre enraciné. Il suffit de choisir un élément comme sommet de l'arbre et de l'organiser de façon à obtenir un arbre enraciné. Voici un exemple d'arbre non enraciné :

Vous remarquerez qu'il y a équivalence entre les deux arbres précédents. En effet, en réorganisant l'arbre non enraciné, on peut obtenir strictement le même arbre que le premier. En revanche, ce n'est qu'un exemple d'arbre enraciné que l'on peut effectuer avec cet arbre non enraciné, il en existera d'autres.

Dans la suite, nous nous intéresserons uniquement aux arbres enracinés.

Précisons maintenant un peu plus les termes désignant les différents composant d'un arbre.

Tout d'abord, chaque élément d'un arbre se nomme un noeud. Les noeuds sont reliés les uns aux autres par des relations d'ordre ou de hiérarchie. Ainsi on dira qu'un noeud possède un père, c'est à dire un noeud qui lui est supérieur dans cette hiérarchie. Il possède éventuellement un ou plusieurs fils.

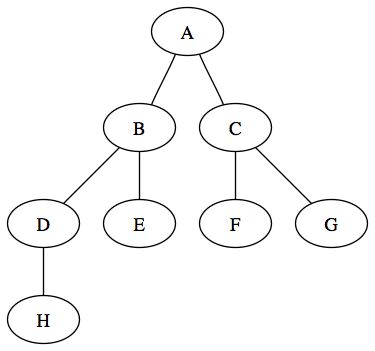
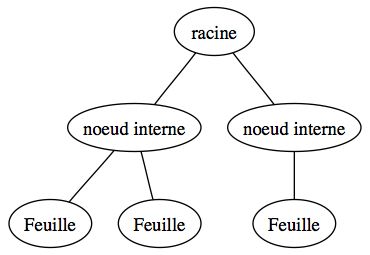
Il existe un noeud qui n'a pas de père, c'est donc la racine de l'arbre. Un noeud qui n'a pas de fils est appelé un feuille. Parfois on appelle une feuille un noeud externe tout autre noeud de l'arbre sera alors appelé un noeud interne.

Voici donc un schéma qui résume les différents composant d'un arbre :

On a aussi envie de qualifier un arbre sur le nombre de fils qu'il possède. Ceci s'appelle l'arité de l'arbre. Un arbre dont les noeuds ne comporteront qu'au maximum n fils sera d'arrité n. On parlera alors d'arbre n-aire. Il existe un cas particulièrement utilisé : c'est l'arbre binaire. Dans un tel arbre, les noeuds ont au maximum 2 fils. On parlera alors de fils gauche et de fils droit pour les noeuds constituant ce type d'arbre.

L'arité n'impose pas le nombre minimum de fils, il s'agit d'un maximum, ainsi un arbre d'arité 3 pourra avoir des noeuds qui ont 0,1,2 ou 3 fils, mais en tout cas pas plus.

On appelle degré d'un noeud, le nombre de fils que possède ce noeud.

La suite de cet article portera uniquement sur les arbres binaires puisque c'est le type d'arbre le plus basique à étudier mais aussi parce que tout ce que vous verrez sur un arbre binaire est valable pour un arbre n-aire.

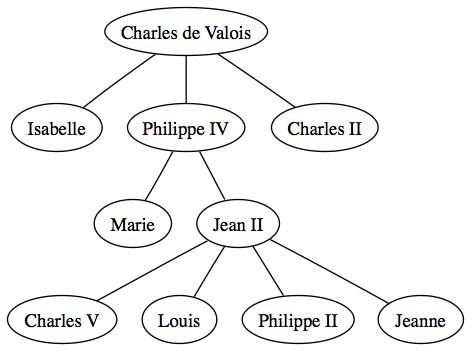
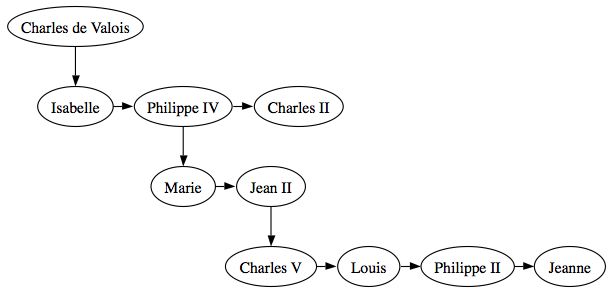
De plus il est possible de passer d'un arbre n-aire à un arbre binaire. Voici un exemple de passage d'un arbre généalogique (qui par définition n'est pas forcément binaire) à un arbre binaire.

Voici donc l'arbre généalogique de base :

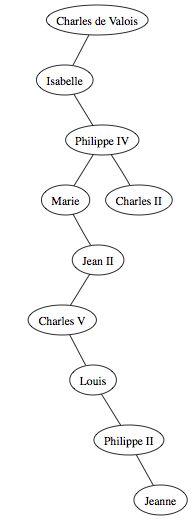
En remarquant qu'on peut mettre sur les fils gauche les enfants et sur les fils droit les frères et soeurs on en déduit donc que l'on peut construire un arbre binaire à partir de l'arbre n-aire. Voici donc l'arbre que nous obtenons :

Comme vous pouvez le constater, il est assez difficile de lire ce genre d'arbre et généralement on remonte au même niveau les noeuds de la même génération. Ainsi un noeud n'a pas de fils gauche et de fils droit mais un fils et un frère. Voici à quoi peut ressembler l'arbre précédent dans ce cas:

On distingue alors mieux les générations : sur la même ligne nous avons les frères et soeurs.

On appelle la taille d'un arbre, le nombre de noeud interne qui le compose. C'est à dire le nombre noeud total moins le nombre de feuille de l'arbre.

On appele également la profondeur d'un noeud la distance en terme de noeud par rapport à l'origine. Par convention, la racine est de profondeur 0. Dans l'exemple suivante le noeud F est de profondeur 2 et le noeud H est de profondeur 3.

La hauteur de l'arbre est alors la profondeur maximale de ses noeud. C'est à dire la profondeur à laquelle il faut descendre dans l'arbre pour trouver le noeud le plus loin de la racine.On peut aussi définir la hauteur de manière récursive : la hauteur d'un arbre est le maximum des hauteur ses fils. C'est à partir de cette définition que nous pourrons exprimer un algorithme de calcul de la hauteur de l'arbre.

La hauteur d'un arbre est très importante. En effet, c'est un repère de performance. La plupart des algorithmes que nous verrons dans la suite ont une complexité qui dépend de la hauteur de l'arbre. Ainsi plus l'arbre aura une hauteur élevée, plus l'algorithme mettra de temps à s'exécuter.

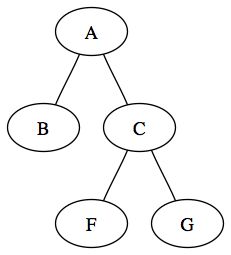
Un arbre binaire localement complet est un arbre binaire dont chacun des noeuds possèdent soit 0 soit 2 fils. Ceci veut donc dire que les noeuds internes auront tous deux fils. Dans ce type d'arbre, on peut établir une relation entre la taille de l'arbre et le nombre de feuille. En effet, un arbre binaire localement complet de taille n aura n+1 feuille. L'arbre suivant est localement complet :

Un arbre dégénéré (appelé aussi filiforme) est un arbre dont les noeuds ne possède qu'un et un seul fils. Cet arbre est donc tout simplement une liste chaînée. Ce type d'arbre est donc à éviter, puisqu'il n'apportera aucun avantage par rapport à une liste chaînée simple. On a alors une relation entre la hauteur et la taille : un arbre dégénéré de taille n a une hauteur égale à n+1. L'arbre suivant est un arbre dégénéré.

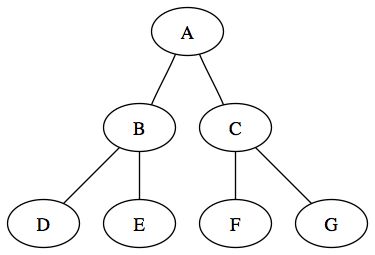
On appellera arbre binaire complet tout arbre qui est localement complet et dont toutes les feuilles ont la même profondeur. Dans ce type d'arbre, on peut exprimer le nombre de noeuds n de l'arbre en fonction de la hauteur h : n = 2^(h+1) -1.

Pour calculer la hauteur d'un arbre, nous allons nous baser sur la définition récursive :

- un arbre vide est de hauteur 0
- un arbre non vide a pour hauteur 1 + la hauteur maximale entre ses fils.

De part cette définition, nous pouvons en déduire un algorithme en pseudo code :

fonction hauteur ( T : arbre ) renvoie un entier

	si T est vide
		renvoyer 0
	sinon
		renvoyer 1 + max (hauteur ( FilsGauche(T)) , hauteur(FilsDroit(T) )
	fin si

Ainsi ceci pourrait donner en C :

unsigned Height (tree T)
{
	if ( IsEmpty(T) )
		return 0;
	else
		return 1 + max( Height(Left(T) ) , Height(Right(T) ) );
}

La fonction max n'est pas définie c'est ce que nous faisons maintenant :

unsigned max(unsigned a,unsigned b)
{
	return (a>b)? a : b ;
}

Le calcul du nombre de noeud est très simple. On définit le calcul en utilisant la définition récursive :

- Si l'arbre est vide : renvoyer 0
- Sinon renvoyer 1 plus la somme du nombre de noeuds des sous arbres.

On aura donc le pseudo code suivant :

fonction NombreNoeud( T : arbre ) renvoie un entier

	si ( EstVide( T ) )
		renvoyer 0;
	sinon
		renvoyer 1 + NombreNoeud(FilsGauche(T)) + NombreNoeud(FilsDroit(T));
	fin si

On peut donc traduire celà en langage C :

unsigned NbNode(tree T)
{
	if( IsEmpty(T) )
		return 0;
	else
		return 1 + NbNode(Left(T)) + NbNode(Right(T));
}

Le calcul du nombre de feuille repose sur la défintion récursive :

- un arbre vide n'a pas de feuille.
- un arbre non vide a son nombre de feuille défini de la façon suivante :
	- si le noeud est une feuille alors on renvoie 1
	- si c'est un noeud interne alors le nombre de feuille est la somme du 
	  nombre de feuille de chacun de ses fils.

Voici le pseudo code que nous pouvons en tirer :

fonction nombreFeuille ( T : arbre ) renvoie un entier

	si T est vide alors
		renvoyer 0;
	sinon si T est une feuille alors 
		renvoyer 1
	sinon
		renvoyer nombrefeuille( FilsGauche(T) ) + nombrefeuille( FilsDroit(T) );
	fin si

Voici ce que celà peut donner en langage C :

unsigned NbLeaves( tree T)
{
	if( IsEmpty(T) )
		return 0;
	else if ( IsLeave(T) )
		return 1;
	else
		return NbLeaves(Left(T)) + NbLeaves(Right(T));
}

Maintenant, pour finir avec les algorithmes de base, nous allons calculer le nombre de noeud interne, Cela repose sur le même principe que le calcul du nombre de feuille. La définition récursive est la suivante :

- un arbre vide n'a pas de noeud interne.
- si le noeud en cours n'a pas de fils alors renvoyer 0
- si le noeud a au moins un fils, renvoyer 1 plus la somme des noeuds interne des sous arbres.

On en déduit donc aisément le pseudo code correspondant :

fonction NombreNoeudInterne(T : arbre ) renvoie un entier

	si EstVide(T) alors
		renvoyer 0
	sinon si EstUneFeuille(T) alors
		renvoyer 0
	sinon 
		renvoyer 1 + NombreNoeudInterne(FilsGauche(T)) +
				NombreNoeudInterne(FilsDroit(T));

Ce qui donne en langage C :

unsigned NbInternalNode(tree T)
{
	if (IsEmpty(T))
		return 0;
	else if(IsLeave(T))
		return 0;
	else
		return 1 + NbInternalNode(Left(T)) + NbInternalNode(Right(T));
}

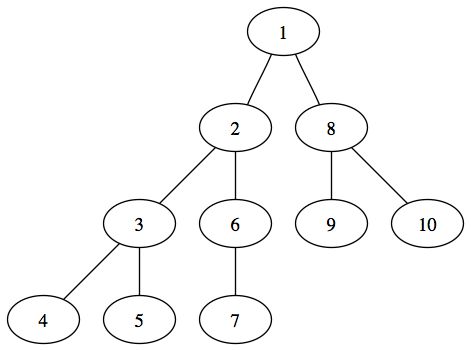
Le parcours en profondeur de l'arbre suivant donne : 1,2,3,4,5,6,7,8,9,10 :

Ceci n'est en fait qu'un seul parcours en profondeur de l'arbre. Il s'agit d'un parcours d'arbre en profondeur à gauche d'abord et préfixe. Précisons. tout de suite ces termes.

Un parcours en profondeur à gauche est simple à comprendre, cela signifie que l'on parcours les branches de gauche avant les branches de droite. On aura dons deux types de parcours : un parcours à gauche et un parcours à droite. Dans la plupart des cas, nous utiliserons un parcours à gauche.

La deuxième caractéristique de notre arbre est le parcours dit préfixe. Celà signifie que l'on affiche la racine de l'arbre, on parcourt tout le sous arbre de gauche, une fois qu'il n'y a plus de sous arbre gauche on parcourt les éléments du sous arbre droit. Ce type de parcours peut être résumé en trois lettres : R G D (pour Racine Gauche Droit). On a aussi deux autres types de parcours : le parcours infixe et le parcours suffixe (appelé aussi postfixe). Le parcours infixe affiche la racine après avoir traité le sous arbre gauche, après traitement de la racine, ontraite le sous arbre droit (c'est donc un parcours G R D). Le parcours postfixe effectue donc le dernier type de schéma : sous arbre gauche, sous arbre droit puis la racine, c'est donc un parcours G D R. Bien sur, nous avons fait l'hypothèse d'un parcours à gauche d'abord mais on aurait pû aussi faire un parcours à droite d'abord.

Les types de parcours infixe,suffixe et postfixe sont les plus importants, en effet chacun à son application particulière. Nous verrons celà dans la suite

Maintenant que nous avons la définition des types de parcours, exprimons ceci en terme de pseudo-code.

Commençons par le parcours préfixe, celui ci traite la racine d'abord.

procedure parcours_prof_prefixe( T : arbre )

	si non EstVide(T) alors
		
		traiter_racine(T);
		parcours_prof_prefixe(FilsGauche(T));
		parcours_prof_prefixe(FilsDroit(T));
	
	fin si

La fonction (ou procédure) traiter_racine, est une fonction que vous définissez vous même, il s'agit par exemple d'une fonction d'affichage de l'élément qui est à la racine.

Maintenant le parcours infixe :

procedure parcours_prof_infixe( T : arbre )

	si non EstVide(T) alors
		
		parcours_prof_infixe(FilsGauche(T));
		traiter_racine(T);
		parcours_prof_infixe(FilsDroit(T));

	fin si

Et enfin le parcours suffixe :

proceure parcours_prof_suffixe(T : arbre )

	si non EstVide(T) alors

		parcours_prof_suffixe(FilsGauche(T));
		parcours_prof_suffixe(FilsDroit(T));
		traiter_racine(T);

	fin si

Voilà pour les trois fonctions de parcours. Vous remarquerez que seul le placement de la fonction (ou procédure) traiter_racine diffère d'une fonction à l'autre. Nous pouvons donc traiter ceci facilement, afin de ne pas à avoir à écrire trois fois de suite le même code. Voici donc le code que l'on peut avoir en C :

void DFS(tree T, char Type)
{
	if( ! IsEmpty(T) )
	{
		if( Type ==1 )
		{
			/* traiter racine */
		}

		DFS(Left(T), Type);

		if (Type == 2)
		{
			/* traiter racine */
		}

		DFS(Right(T), Type);	
		
		if( Type == 3)
		{
			/* traiter racine */
		}
	}
}

Ainsi à partir de ce code, on peut facilement créer trois fonctions qui seront respectivement le parcours préfixe, le parcours infixe et le parcours suffixe.

void DFS_prefix(tree T)
{
	DFS(T,1);
}

void DFS_infix(tree T)
{
	DFS(T,2);
}

void DFS_postfix(tree T)
{
	DFS(T,3);
}

Nous allons aborder un type de parcours un peu plus compliqué, c'est le parcours en largeur. Il s'agit d'un parcours dans lequel, on traite les noeuds un par un sur un même niveau. On passe ensuite sur le niveau suivant, et ainsi de suite. Le parcours en largeur de l'arbre suivant est : 1 2 3 4 5 6 7 8 9 10.

Une méthode pour réaliser un parcours en largeur consiste à utiliser une structure de données de type file d'attente. Pour ceux qui ne connaissent pas encore ce type de structure de données, il s'agit tout simplement d'une structure de données qui est obéit à la règle suivante : premier entrée, premier sorti.

Pour en revenir à notre parcours, le principe est le suivant, lorsque nous somme sur un noeud nous traitons ce noeud (par exemple nous l'affichons) puis nous mettons les fils gauche et droit non vides de ce noeud dans la file d'attente, puis nous traitons le prochain noeud de la file d'attente.

Au début, la file d'attente ne contient rien, nous y plaçons donc la racine de l'arbre que nous voulons traiter. L'algorithme s'arrête lorsque la file d'attente est vide. En effet, lorsque la file d'attente est vide, cela veut dire qu'aucun des noeuds parcourus précédemment n'avait de sous arbre gauche ni de sous arbre droit. Par conséquent, on a donc bien parcouru tous les noeuds de l'arbre.

On en déduit donc le pseudo code suivant :

procedure parcours_largeur(T : arbre)

	Creer_File_D'attente F

	ajouter(F,T);

	tant que F n'est pas vide faire 
		X <- extraire(F);
		Traiter_racine(X);
	
		si non EstVide(FilsGauche(X)) alors
			ajouter(F,FilsGauche(X));
		fin si
	
		si non EstVide(FilsDroit(X)) alors
			ajouter(F,FilsDroit(X));
		fin si

	fin faire

Appliquons ce pseudo code à l'arbre suivant :

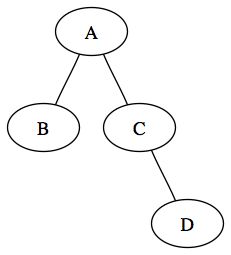
Au tout début de l'algorithme, la file ne contient rien, on y ajoute donc l'arbre, la file d'attente devient donc :

On traite la racine puis on y ajoute les fils droits et gauche, la file vaut donc :

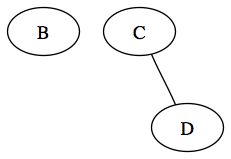
On traite ensuite le prochain élément de la file d'attente. Ce noeud n'a pas de sous arbre, on ajoute donc rien à la file. Celle ci vaut donc :

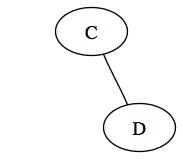
On traite le prochain noeud dans la file d'attente. Celui ci a un fils droit, nous l'ajoutons donc à la file d'attente. Cette dernière ne contient donc maintenant plus qu'un noeud :

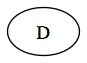
On traite ce noeud. Celui ci n'ayant pas de fils, nous n'ajoutons donc rien à la file. La file est désormais vide, l'algorithme se termine.

Nous pouvons écrire cet algorithme en langage C. Cependant, nous n'avons pas vu les files dans cet article, je vous renvoie donc à l'article de Nicolas Joseph sur la création des files d'attentes en C Ici Nous ne rentrerons pas plus en détail sur les files dans la suite. Voici donc le code en C :

void WideSearch(tree T)
{
	tree Temp;
	queue F;
	
	if( ! IsEmpty(T) )
	{
		Add(F,T);

		while( ! Empty(F) )
		{
			Temp = Extract(F);
			
			/* Traiter la racine */
			if( ! IsEmpty(Left(Temp)) )
				Add(F,Temp);
			if( ! IsEmpty(Right(Temp)) )
				Add(F,Temp);
		}
	}
}

On peut distinguer deux types de création d'un arbre : création d'un arbre vide, et création d'un arbre à partir d'un élément et de deux sous arbres. La première méthode est très simple, étant donné que nous avons crée un arbre comme étant un pointeur, un arbre vide est donc un pointeur Null. La fonction de création d'un arbre vide est donc une fonction qui nous renvoie la constante Null.

La deuxième fonction est un peu plus compliquée mais rien de très impressionnant. Il faut tout d'abord créer un noeud, ensuite, on place dans les fils gauche et droit les sous arbres que l'on a passé en paramètre ainsi que la valeur associée au noeud. Enfin, il suffit de renvoyer ce noeud. En fait, ce n'est pas tout à fait exact, puisque ce n'est pas un noeud mais un pointeur sur un noeud qu'il faut renvoyer. Mais nous utilisons le terme noeud pour spécifier qu'il faut allouer un noeud en mémoire.

Voici le pseudo code de la deuxième fonction :

fonction CreerArbre(val : TElement, fg : arbre , fd : arbre ) renvoie un arbre

	X <- Allouer un noeud en mémoire.

	X.valeur <- val;
	X.fils_gauche <- fg;
	X.fils_droit <- fd;

	renvoyer X;

Ceci donnera donc en langage C :

tree Create(TElement val,tree ls, tree rs)
{
	tree res;

	res = malloc(sizeof(*res));

	if( res == NULL )
	{
		fprintf(stderr,"Impossible d'allouer le noeud");
		return NULL;
	}

	res->value = val;
	res->left = ls;
	res->right = rs;

	return res;
}

Notre fonction renvoie NULL s'il a été impossible d'allouer le noeud. Ceci est un choix arbitraire, vous pouvez très bien effectuer d'autres opérations à la place.

L'ajout d'un élément est un peu plus délicat. En effet, il faut distinguer plusieurs cas : soit on insère dès que l'on peut. soit on insère de façon à obtenir un arbre qui se rapproche le plus possible d'un arbre complet, soit on insère de façon à garder une certaine logique dans l'arbre.

Le premier type d'ajout est le plus simple, dès que l'on trouve un noeud qui a un fils vide, on y met le sous arbre que l'on veut insérer. Cependant ce type de technique, si elle sert à construire un arbre depuis le début à un inconvénient : on va créer des arbres du type peigne. C'est à dire que l'on va insérer notre élément tel que l'arbre final ressemblera à ceci :

Ceci est très embêtant dans la mesure ou celà va créer des arbres de très grande hauteur, et donc très peu performant. Néanmoins, il peut arriver des cas où on a parfois besoin de ce type d'insertion. Dans ce cas, l'insertion se déroule en deux temps : on cherche d'abord un fils vide, puis on insère. Ceci peut s'écrire récursivement :

- si l'arbre dans lequel on veut insérer notre élément est vide, 
	alors il s'agit d'une création d'arbre.
- sinon, si le noeud en cours a un fils vide, alors on insère dans le fils vide.
	   -sinon, on insère dans le fils gauche.

Vous remarquerez que l'on insère du coté gauche, ceci aura pour effet de produire un peigne gauche, et si on insérait du coté droit, nous aurions un peigne droit.

Nous pouvons donc écrire le pseudo code correspondant :

procedure AjouteNoeud( src : arbre, elt : TElement )

	si EstVide(src) alors
		src <- CreerArbre(elt,Null,Null);
	sinon
		si EstVide(FilsGauche(src)) alors
			src->gauche <- CreerArbre(elt,Null,Null);
		sinon 
			si EstVide(FilsDroit(src)) alors
				src->droit <- CreerArbre(elt,Null,Null);
			sinon
				AjouteNoeud(FilsGauche(src),elt);
			fin si
		fin si
	fin si

On peut traduire ceci en C :

void AddElt(tree src, TElement elt)
{
	if ( src == NULL )
	{
		src = Create(elt,NULL,NULL);
	}
	else if ( IsEmpty(Left(src)) )
	{
		src->left = Create(elt,NULL,NULL);
	}
	else if ( IsEmpty(Right(src)) )
	{
		src->right = Create(elt,NULL,NULL);
	}
	else
	{
		AddElt(Left(src),elt);
	}
}

On remarque donc qu'ici nous créons des arbres qui ne sont pas perfomant (nous verrons ceci dans la recherche d'élément). Afin d'améliorer ceci, on peut éventuellement effectuer notre appel récursif soit à gauche soit à droite et ceci de façon aléatoire. Ceci permet un équilibrage des insertions des noeuds mais ce n'est pas parfait.

La solution pour obtenir des arbres les plus équilibrés possible consiste en l'utilisation d'arbres binaires dit rouge-noir. Ceci sont assez compliqué et nous ne les verrons pas. Cependant, nous allons voir un type d'arbre qui facilite les recherche : les arbres binaires de recherche.

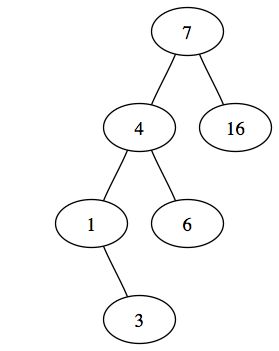
Dans ce type d'arbre, il y a une cohérence entre les noeuds, c'est à dire que la hierarchie des noeuds respecte une règle. Celle ci est simple. Pour un arbre binaire de recherche contenant des entiers, nous considérerons que les valeurs des noeuds des sous arbres gauche sont inférieur à la racine de ce noeud et les valeurs des sous arbres droit sont suppérieurs à cette racine. Voici un exemple d'un tel arbre :

Puisque nous sommes dans la partie ajout de noeud, voyons comment ajouter un noeud dans un tel arbre :

procedure InsereArbreRecherche( src : arbre , elt : TElement )

	si EstVide(src) alors
		src <- CreerArbre(elt,Null,Null);
	sinon
		si elt < src->val alors
			InsereArbreRecherche(FilsGauche(src), elt);
		sinon
			InsereArbreRecherche(FilsDroit(src), elt);
		fin si
	fin si

Le principe d'insertion est simple : si on a un arbre vide, alors il s'agit de la création d'un arbre. Sinon, on compare la valeur de l'élément à insérer avec la valeur de la racine. Si l'élément est plus petit alors on insère à gauche. sinon, on insère dans le fils droit de la racine.

Voici le code en C que l'on peut écrire pour insérer un élement dans un arbre binaire de recherche.

void insertSearchTree(tree src, TElement elt)
{
	if( IsEmpty(src) )
	{
		src = Create(elt,NULL,NULL);
	}
	else
	{
		if (elt < src->value)
		{
			insertSearchTree(Left(src), elt);
		}
		else
		{
			insertSearchTree(Right(src), elt);
		} 
	}
}

Vous remarquerez que l'on insère les éléments qui sont égaux à la racine du coté droit de l'arbre.

Autre remarque, vous constaterez que nous effectuons des comparaisons sur les entités du type TElement, ceci n'est valable que pour des valeurs numériques (entier, flottant et caractère). S'il s'agit d'autres types, vous devrez utiliser votre propre fonction de comparaison. (comme strcmp pour les chaînes de caractère).

Après avoir alimenté notre arbre, il serait peut être temps d'effectuer des recherches sur notre arbre. Il ya principalement deux méthodes de recherche. Elles sont directement liées au type de l'arbre : si l'arbre est quelconque et si l'arbre est un arbre de recherche.

Nos recherches se contenterons seulement de déterminer si la valeur existe dans l'arbre. Avec une petite adaptation, on peut récupérer l'arbre dont la racine contient est identique à l'élément cherché.

Commençons par chercher l'élement dans un arbre quelconque. Cette méthode est la plus intuitive : on cherche dans tous les noeuds de l'arbre l'élement. Si celui ci est trouvé, on renvoie vrai, si ce n'est pas le cas, on renvoie faux. Voici le pseudo code associé.

fonction Existe(src : arbre, elt : TElement) renvoie un booléen

	si EstVide(src)
		renvoyer faux
	sinon
		si src->value = elt alors
			renvoyer vrai
		sinon
			renvoyer Existe(FilsGauche(src),elt ) ou Existe(FilsDroit(src), elt);
		fin si
	sin si

Nous renvoyons un ou logique entre le sous arbre gauche et le sous arbre droit, pour pouvoir renvoyer vrai si l'élement existe dans l'un des sous arbres et faux sinon.

Ce genre de recherche est correcte mais n'est pas très performante. En effet, il faut parcourir quasiment tous les noeuds de l'arbre pour déterminer si l'élément existe.

C'est pour celà que sont apparus les arbres binaires de recherche. En effet, on les nomme ainsi parce qu'ils optimisent les recherches dans un arbre. Pour savoir si un élément existe, il faut parcourir seulement une branche de l'arbre. Ce qui fait que le temps de recherche est directement proportionnel à la hauteur de l'arbre.

L'algorithme se base directement sur les propriétés de l'arbre, si l'élement que l'on cherche est plus petit que la valeur du noeud alors on cherche dans le sous arbre de gauche, sinon, on cherche dans le sous arbre de droite. Voici le pseudo code correspondant :

fonction ExisteR( src : arbre, elt : TElement )

	si EstVide(src) alors
		renvoyer faux
	sinon
		si src->valeur = elt alors
			renvoyer vrai;
		sinon
			si src->valeur > elt alors
				renvoyer ExisteR(FilsGauche(src) , elt );
			sinon
				renvoyer ExisteR(FilsDroit(src) , elt );
			fin si
		fin si
	fin si

Ce qui se traduit de la façon suivante en langage C :

bool Exist(tree src , TElement elt)
{
	if ( IsEmpty(src) )
		return false;
	else if ( src->value == elt )
		return true;
	else if ( src->value > elt )
		return Exist(Left(src), elt);
	else
		return Exist(Right(src), elt);
}

Nous allons terminé cet article par la suppression d'éléments d'un arbre, ou plutôt la destruction complète d'un arbre.

Par suppression de noeud, nous entendrons suppression d'une feuille. En effet, un noeud qui possède des fils s'il est supprimé, entraîne une réorganisation de l'arbre. Que faire alors des sous arbres du noeud que nous vollons supprimer ? La réponse à cette question dépend énormément du type d'application de l'arbre. On peut les supprimer, on peut réorganiser l'arbre (si c'est un arbre de recherche) en y insérant les sous arbres qui sont devenus orphelins. Bref, pour simplifier les choses, nous allons nous contenter de supprimer completement l'arbre.

L'algorithme de suppression de l'arbre est simple : on supprime les feuilles une par unes. On répète l'opération autant de fois qu'il y a de feuilles. Cette opération est donc très dépendante du nombre de noeud.

En fait cet algorithme est un simple parcours d'arbre. En effet, lorsque nous devrons traiter la racine, nous appelerons une fonction de suppression de la racine. Comme nous avons dis plutôt que nous ne supprimerons que des feuilles, avant de supprimer la racine, il faut supprimer les sous arbres gauche et droit. On en déduit donc que l'algorithme de suppression est un parcours d'arbre postfixe.

Voici le pseudo code associé :

procedure supprime( src : arbre )

	si non EstVide(src) alors
		supprime(FilsGauche(src));
		supprime(FilsDroit(src));
		supprimeNoeud(src);
	fin si

Le pseudo code est donc très simple. De la même manière, on en déduit le code en C :

void Erase(tree * src)
{
	tree ls = Left(*src);
	tree rs = Right(*src);
	
	if( ! IsEmpty(*src) )
	{
		Erase( &ls );
		Erase( &rs );

		free( *src );
		*src = NULL;
	}
}

On peut se demander pourquoi nous passons par un pointeur sur un arbre pour effectuer notre fonction. Ceci est tout simplement du au fait que le C ne fait que du passage de paramètre par copie et par conséquent si on veut que l'arbre soit réelement vide (ie : qu'il soit égal à NULL) après l'éxécution de la fonction, il faut procéder ainsi.

Les appels à Left et Right au début ne posent aucun problème dans le cas où src vaut NULL. En effet, dans ce cas, les deux fonctions renverrons le pointeur NULL.