I. Introduction▲
Cet article est le premier d'une série d'article consacré à la théorie des graphes. Il est dédié à l'introduction de notions sur les graphes.
Les graphes sont très utilisés dans l'informatique. On les trouve partout : les réseaux, l'ordonnancement de processus, ... . Mais ils sont surtout utilisés pour modéliser des problèmes plus ou moins complexes. Ainsi on pourra représenter un réseau de chemin de fer ou un réseau routier. Et ensuite on peut se servir de cette modélisation pour résoudre des problèmes tels que la recherche du plus court chemin entre deux villes.
La théorie des graphes est très probablement née en 1735 lorsque Leonhard Euler (1707 - 1783) résout le problème des sept ponts de Königsberg (De nos jours Kaliningrad en Russie). Ce problème est très simple sur le principe mais un peu plus compliqué à démontrer, en voici l'énoncé : La vile de Königsberg est une ville autour d'un fleuve, elle compte quatre berges et sept ponts les reliant. Le but du jeu est de savoir s'il existe un chemin permettant d'emprunter tous les ponts une fois et une seule et revenir au point de départ. Le problème s'appelle, de façon plus formelle, la recherche d'un cycle eulérien dans un graphe. Euler a démontré que ce problème n'avait pas de solution.
I-A. Définitions générales▲
Un graphe est composé de sommets et d'arcs (ou d'arêtes, nous verrons cela un peu plus tard). Un graphe G est défini de manière formelle par un couple (S,A) où :
- S est un ensemble fini d'éléments. Chacun de ces éléments est appelé sommet du graphe.
- A est un sous ensemble (éventuellement nul) de SxS. Chacun de ces éléments de A est appelé arc ou arête.
L'ensemble A est donc composé de paires (x,y), x et y étant appelés les extrémités de l'arête (ou de l'arc). Cette définition peut paraître très vague, voici donc un exemple de graphe :
Dans les ronds, nous avons donc les sommets. Ceux-ci sont reliés entre eux par des arcs. Quelques fois les sommets sont appelés des noeuds. Ces deux définitions sont totalement identiques.
On appellera taille du graphe, le cardinal de l'ensemble A, c'est à dire le nombre d'arêtes du graphe. De même, on appelle ordre, le cardinal de l'ensemble S, c'est à dire le nombre de sommets du graphe.
Graphes orientés - Graphes non orientés▲
Il convient de distinguer deux grands types de graphes : les graphes orientés et ceux qui ne le sont pas (les graphes non orientés).
Un graphe orienté est un graphe dont les arêtes sont orientées. Cela signifie que les extrémités d'une arête ont un sens bien précis. On appellera alors l'arête un arc. Les extrémités de l'arc sont alors appelés extrémité initiale et extrémité finale. Un arc (x,y) sera donc l'arc pour lequel x est l'extrémité initiale et y l'extrémité finale.
Conventionnellement un arc sera représenté entre parenthèses et une arête sera représenté entre accolades. Concrètement, cela signifie qu'un graphe orienté ne permet le passage d'un sommet à un autre que dans un seul sens.
D'une manière plus concrète encore, imaginez un réseau routier représenté par un graphe orienté. Dans ce cas, cela signifiera que les routes seront à sens unique. Dans un graphe non orienté les routes seront à double sens.
Il arrive parfois qu'on parle de graphe associé à un graphe orienté, ce graphe non orienté n'est rien d'autre que le graphe orienté auquel on a remplacé les arcs par des arêtes. On utilise quelque fois ce genre de graphe pour faciliter les opérations et déduire des propriétés facilement.
Multigraphes - Hypergraphes - Pseudographes - Digraphes.▲
Avant d'aller plus loin dans les définitions des graphes, on trouve plusieurs noms pour identifier les graphes .
Parmi ces noms on trouve le terme d'Hypergraphe. Un hypergraphe est la structure mathématique qui généralise la théorie des graphes. Dans un hypergraphe, une même arête peut connecter plusieurs sommets. Dans ce cas, on parlera d'hyperarête. Les hypergraphes sont des objets plutôt compliqués à comprendre et à utiliser, nous en donnons seulement son nom et nous n'en parlerons plus.
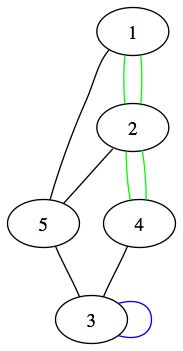
Un pseudographe est un graphe pour lequel on peut avoir des arêtes parallèles et aussi des boucles.
Deux arrêtes a(x,y) et a2(x',y') sont parallèles si x = x' et y = y'. Cela signifie tout simplement qu'il existe deux arêtes différentes pour relier deux sommets.
On appelle boucle, une arrête dont le sommet de départ est aussi le sommet d'arrivée. Voici donc en vert deux arrêtes parallèles et en bleu une boucle.
Un pseudographe est donc un type particulier de graphe qui peut comporter ces deux types d'arêtes. On trouve également le nom de multigraphe pour identifier ce type de graphe. Les mathématiciens eux-mêmes ne sont pas d'accord entre eux pour savoir la vraie propriété d'un multigraphe et d'un pseudographe. Ne portez donc pas de réclamation sur ces définitions, nous ne le savons pas non plus et de plus il ne semble pas y avoir pas de définition précise.
Enfin, pour le terme digraphe, sachez qu'il s'agit tout simplement d'un synonyme de graphe orienté. Ce sont donc deux définitions strictement équivalentes. Nous utiliserons le terme graphe orienté tout simplement parce qu'il est plus parlant.
Chaînes - Chemin - Circuit - Cycle.▲
On appelle deux sommets adjacents deux sommets qui sont reliés par une arête. C'est à dire que l'on peut passer de l'un à l'autre directement sans passer par d'autres sommets.
Dans le graphe suivant, les sommets 1 et 3 sont adjacents :
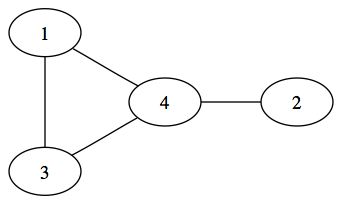
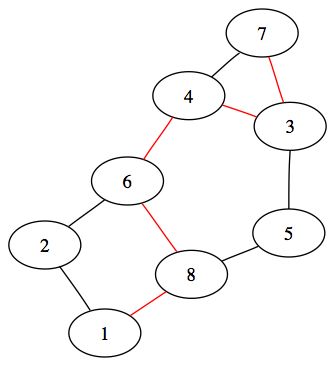
On appelle chaîne, une suite de sommets adjacents, c'est à dire une suite de sommet reliés par des arêtes. La longueur de la chaîne est le nombre d'arêtes visitées pour passer du premier sommet de la chaîne au dernier. On appelle chaîne simple, une chaîne qui n'est composée que de sommets différents
Nous voyons en rouge dans le graphe suivant une chaîne :
On appelle chemin une suite de sommets reliés par des arcs. C'est donc la définition d'une chaîne pour les graphes orientés. Comme pour les chaînes, on appelle chemin simple tout chemin qui ne passe pas deux fois par le même sommet.
Un circuit est un chemin fermé simple. On entend par chemin fermé un chemin dont le sommet initial est aussi le sommet final. Voici par exemple un circuit :
On appelle cycle une chaîne fermée. C'est donc un circuit pour les graphes non orientés. Il est dit élémentaire si la chaîne sur laquelle il est basé est simple (hormis le sommet de départ et d'arrivé, cela va de soit.).
On appelle une foret un graphe qui ne possède pas de cycle.
Il existe principalement deux qualificatifs pour les chemins et les chaînes. Ces deux qualificatifs sont eulérien et hamiltonien.
Un circuit ou une chaîne est eurélien(ne) si toutes les arêtes du graphe y apparaissent une fois et une seule.
Les chemins ou les chaînes sont dit hamiltonen(ne) si tous les sommets du graphes y apparaissent une fois et une seule.
Le problème des sept ponts de Königsberg était de trouver un circuit eulérien dans le graphe. En effet, le but était de trouver un circuit qui passe par tous les ponts. C'est d'ailleurs en hommage à Euler que l'on appelle ceci un circuit eulérien.
La recherche d'un cycle hamiltonien peut être utilisé par exemple dans la vie moderne lorsque l'on veut à partir d'une carte routière passer par une liste de ville.
Graphe complet - graphe connexe - fortement connexe - graphe planaire ▲
Un graphe est dit complet si tous les sommets, pris deux à deux, sont adjacents. Voici un exemple de graphe complet à quatre sommets :
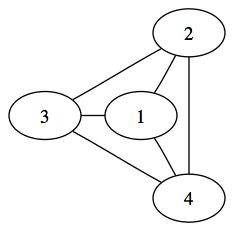
On nomme un graphe complet à n sommets un Kn graphe. La lettre K est en hommage à Kuratowski , un père de la théorie des graphe. Un graphe sera dit connexe s'il existe pour chaque paire de sommet une chaîne reliant chacun des deux sommets. Voici un exemple de graphe connexe :
De même on définit un graphe fortement connexe comme étant un graphe orienté dont toutes les paires de sommets peuvent être reliées par un chemin.
Un dernier type de graphe dont nous parlerons est le graphe planaire. Un graphe planaire d'une manière imagée est un graphe que l'on peut dessiner sans que les arêtes ou les arcs ne se croisent. La recherche de tels graphes est très importante dans les domaines de l'électronique. En effet, dans ce genre d'application il s'agit de réaliser des circuits sans croisement.
Il existe des relations, notament dues à Euler, concernant les graphes connexes planaires et leur nombre d'arêtes et de sommets. On peut par exemple démontrer qu'un graphe connexe est planaire en fonction de son nombre d'arêtes et de sommets. Ceci est assez technique et compliqué, nous ne l'aborderons dans cette introduction.
Degré - voisinage▲
On appelle voisinage d'un graphe, l'ensemble des sommets adjacents du graphe. C'est à dire la liste des sommets que l'on peut directement accéder depuis le sommet courant. Ce concept s'applique uniquement pour les graphes non orientés (nous rappelons que le concept d'adjacence est seulement valable pour les graphes non orientés).
On définit donc pour un graphe orienté deux concepts : les prédécesseurs et les successeurs. Les prédécesseurs d'un sommet sont la liste des sommets depuis lesquels on peut arriver au sommet courant. Les successeurs du sommet sont les sommets auxquels on peut accéder à partir du sommet courant.
Le degré d'un sommet est le nombre d'arêtes qui entrent et qui sortent du sommet en cours. Pour un graphe non orienté, ceci correspond tout naturellement au cardinal de son voisinage.
Pour un graphe orienté, on définit le degré comme étant la somme de deux demi-degrés, le demi degré extérieur et le demi degré intérieur. Le demi-degré intérieur est le cardinal des prédécesseurs du sommet. Par analogie, le demi degré extérieur est le cardinal des successeurs du sommet.
On définit également le degré d'un graphe comme étant le maximum des degrés du graphe. Un graphe de degré 4 aura des sommets dont le degré maximum peut être 4.
Sous graphe - graphe partiel - stable - clique▲
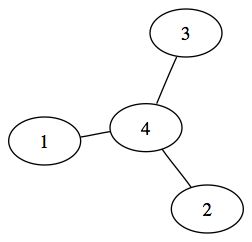
On appelle un sous-graphe d'un graphe un graphe dont on a enlevé des sommets. On y enlève aussi les arêtes qui faisaient référence aux sommets qui ont été enlevés.
Voici donc un graphe et un sous graphe.
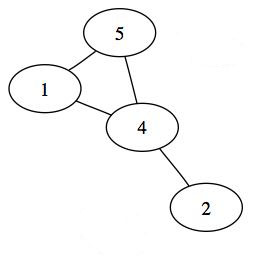
On appelle aussi graphe partiel un graphe auquel on a enlevé des arêtes (ou des arcs). Les deux graphes suivants représentent respectivement un graphe et un graphe partiel obtenu à partir de ce graphe :
En combinant ces deux définitions, on peut définir un sous graphe partiel. Il s'agit donc d'un graphe partiel d'un sous graphe. C'est concrètement un graphe auquel on a enlevé des sommets et leurs arêtes incidentes.
On appelle stable, un sous graphe qui n'a pas d'arête. On appelle nombre de stabilité, l'ordre du plus grand stable. Il s'agit donc du nombre maximal de sommets restants après avoir enlevé certains sommets et leurs arêtes incidentes.
Il existe des sous graphes particuliers. En effet, on peut citer les composantes connexes et les cliques.
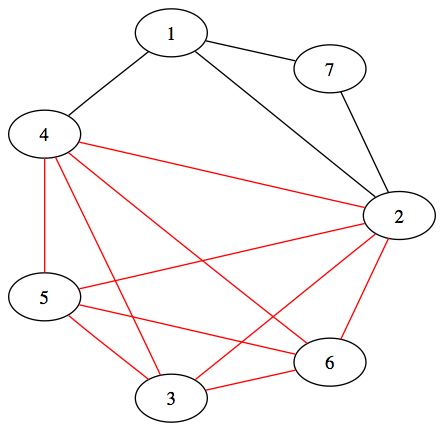
On appelle composante connexe, un sous graphe qui est connexe. Il peut y avoir plusieurs composantes connexes dans un graphe. Cependant, la composante connexe est le plus grand sous graphe que l'on peut obtenir. Par conséquent, la composante connexe d'un graphe connexe est ce même graphe.
Voici en rouge et en bleu deux composantes connexes du graphe :
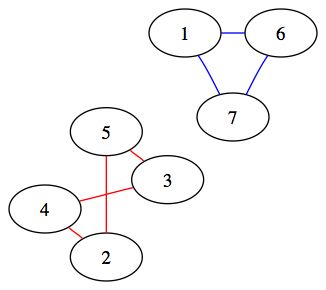
De même, une clique est un sous graphe complet. Voici un exemple en rouge de clique :
Graphes pondérés - graphes probabilistes.▲
On appelle un graphe pondéré, un graphe, orienté ou non, dont les arêtes (ou les arcs) possèdent un poids. C'est à dire que les arêtes possèdent un nombre qui identifie le coût de passage d'un sommet à un autre. Cette pondération est utilisé par exemple dans la représentation d'un réseau routier pour indiquer le temps ou la distance joignant deux villes.
Quelques fois, on nomme les pondérations des valuations. Dans ce cas, les graphes sont dits graphes valués.
Il existe un type de graphe pondéré un peu spécial, on l'appelle graphe probabiliste. Dans ce type de graphe,
la somme des pondérations des arêtes sortantes est égale à un. C'est à dire que si on a deux arêtes sortantes d'un sommet,
la somme de leur pondération est égale à un. Attention toutefois, les pondérations sont dans ce type de graphe comprises entre
0 et 1. On ne pourra donc pas avoir une arête sortante de poids 2 et l'autre -1.
Voilà donc pour les définitions de base sur les graphes. Plutôt indigeste il est vrai mais à force d'utiliser ces termes, vous en deviendrez vite familiers.
I-B. Représentation des graphes▲
Matrices d'adjacence▲
La représentation par matrice d'adjacence consiste en l'utilisation d'une matrice carré ayant pour taille le nombre de sommets du graphe. Sur les lignes et les colonnes on trouve les nom des sommets. En général, on donne des numéros aux sommets, ce qui facilite la lecture.
Considérons la matrice M[n,n], le coefficient M(i,j) qui est le coefficient à l'intersection de la ligne i et de la colonne 1 peut prendre deux valeurs : soit 1 soit 0. Elle vaut 1 si l'arc (i,j) existe c'est à dire qu'il existe un arc reliant le sommet i au sommet j. Elle vaut alors 0 s'il n'y a pas d'arc.
Voici donc un exemple de graphe et de sa matrice d'incidence associée :
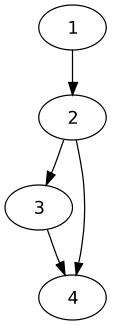
|

|
On remarque aisément qu'un graphe non orienté sera représenté par une matrice symétrique.
Si jamais on est en présence d'un graphe valué, la représentation change quelque peut.
Dans ce type de graphe, il suffit tout simplement de mettre dans le coefficient M(i,j) la valeur de l'arc (i,j). En revanche, il faudra faire attention puisque la valeur 0 peut être utilisée pour valuer le graphe. On utilisera alors une valeur spéciale pour indiquer qu'il n'y a pas de chemin. Quelque fois, il s'agit d'une valeur négative si les valuations sont toutes positives. D'une manière algorithmique, on pourrait utiliser la valeur infinie pour définir la non-existence entre deux sommets. La valeur sera donc choisie en fonction de l'application.
Voici un exemple de graphe valué et de sa matrice associée :
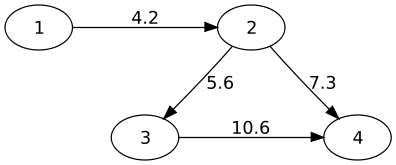
|

|
Listes d'adjacences▲
Une autre idée pour représenter les matrices en mémoire : les listes d'adjacences. Dans ce type de structure, on a un tableau de liste de sommet. Le tableau comporte autant de cases qu'il y a de sommets. Chacune des cases pointe vers une liste de sommet. Cette liste n'est rien d'autre que les successeurs du sommet considéré.
Voici un exemple de graphe et sa liste d'adjacence associée :

|
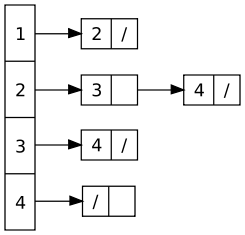
|
Pour un graphe valué, il faut mémoriser dans les noeuds de la liste la valeur du noeud. On peut donc avoir le graphe valué précédent et sa liste d'adjacence associée :

|
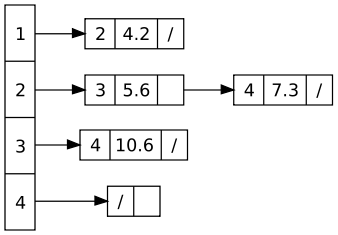
|
On peut se demander pourquoi il y a deux représentations pour les matrices. Cette explication est due principalement à un problème lié à l'informatique : l'espace de stockage. En effet, cet espace bien que de plus en plus important est toujours limité.
Pour une matrice d'adjacence, on constate que l'on stocke des informations dont on n'a pas besoin. En effet, on stocke toutes les liaisons possibles entre les sommets : les arêtes qui existent et même les arêtes qui n'existent pas. De plus, l'espace de stockage nécessaire est directement proportionnel au carré du nombre de sommets du graphe.
Pour une liste d'adjacence, on ne stocke que ce dont on a besoin : que les arêtes qui existent. Ceci rend le stockage directement proportionnel au nombre d'arête et au nombre de sommet.
On peut se dire alors pourquoi ne pas utiliser toujours les listes d'adjacences ? Tout simplement parce qu'elles sont moins efficaces dans certaines conditions. En effet, pour tester si une arête existe entre deux sommets, ceci se fait de manière directe avec une matrice tandis qu'avec une liste, ceci est plus long.
Pour une matrice, tester l'existence d'un arc entre le sommet i et le sommet j, il faut tout simplement tester si le coefficient M(i,j) est différent de 0 (ou d'une valeur particulière comme nous l'avons dit plus haut). D'une façon plus formelle, on dira que cette opération s'effectue en O(1).
Avec une liste d'adjacence, il faut parcourir toute la liste et regarder si le noeud correspond à l'arête que l'on cherche. Si on a de la chance, on tombe directement sur le noeud et on conclut en une seule opération. Cependant, dans le cas le plus défavorable, il faut parcourir toute la liste. Ce cas intervient lorsque l'arc n'existe pas ou qu'il est à la fin de la liste. D'une façon formelle, on peut facilement déduire que cette opération s'effectue en moyenne en O(n/2) où n est le cardinal des successeurs du sommet considéré.
Ceci est un exemple de cas où les matrices sont plus performantes que les listes d'adjacence. Mais alors quand utiliser l'une au profit de l'autre ? D'une manière générale, on considère que si le graphe a peu d'arêtes, il faut mieux utiliser une liste d'adjacence plutôt qu'une matrice (qui serait creuse). En revanche, s'il y a beaucoup d'arêtes, une matrice d'adjacence sera un bon choix.