La théorie des graphes

Le parcours en largeur consiste comme nous venons de le dire à parcourir le graphe en passant par les sommets directement voisins puis ceux dont il faut passer par un sommet pour les atteindre, et ainsi de suite.

Les informations à  prendre en compte pour ce type de parcours sont :

• - Un sommet déjà  visité ne doit pas être revisité.
• - On explore les sommets successeurs directs.

L'algorithme de base repose sur l'utilisation d'une pile qui va maintenir à jour la liste des sommets à visiter.

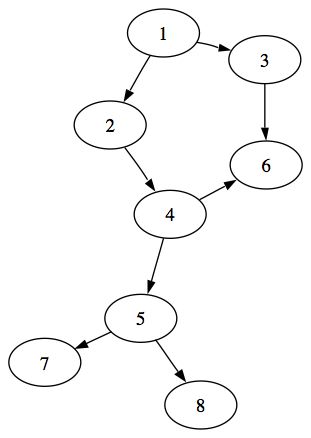
Prenons le graphe suivant :

Imaginons que nous voulions parcourir le graphe en largeur en partant du sommet 1. Le parcours en largeur de ce graphe donnerait la liste suivante : 1 2 3 4 6 5 7 8. Une autre solution serait la suivante : 1 3 2 6 4 5 8 7. Elles sont toutes les deux valables.

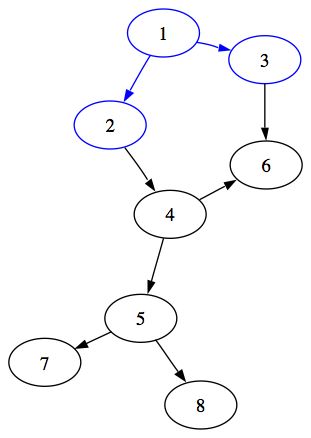
Détaillons un peu comment se déroule le parcours. On part du sommet 1, on liste tous les sommets successeurs, il s'agit donc des sommets 2 et 3. Marquons les d'une couleur différente pour ne pas les passer deux fois :

Il n'y a plus de sommets directement accessibles à partir du sommet 1. Il faut donc maintenant chercher ceux qui sont accessibles en passant par un sommet. Ceci revient en fait à chercher les successeurs des sommets précédemment parcourus. On doit donc parcourir à nouveau en largeur mais en partant des sommets précedemment explorés.

On commence par le sommet 2, le seul successeur est le sommet 4, on l'affiche et on le marque comme étant parcouru. On passe au sommet 3, tout comme le sommet 2, il n'a qu'un seul successeur. On le marque comme déjà  parcouru.

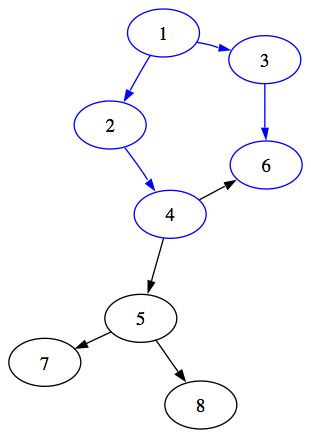
A ce stade, nous en sommes ici :

On vient donc de parcourir tous les sommets accessibles depuis le sommet 1 en passant par un sommet. Il faut donc maintenant parcourir les commets accessibles en passant par deux sommets.

Il faut donc parcourir en partant des sommets 4 et 6. Le sommet 4 a deux successeurs, le sommet 5 et le sommet 6. Or le sommet 6 a déjà été visité, on ne doit donc pas le mettre dans la file des sommets à parcourir. On ajoutera seulement le sommet 5 à la file des sommets à parcourir.

Concernant le parcours à partir du sommet 6, il n'y a rien à faire, en effet, celui ci n'a pas de successeurs.

On réitère le processus jusqu'à avoir parcouru tous nos sommets.

Essayons maintenant de dégager un algorithme de cet exemple. Il parait assez clair qu'il faut avoir une file pour stocker la liste des sommets à parcourir et qu'il nous faut un moyen d'identifier les sommets déjà parcourus.

Pour identifier les sommets parcourus, habituellement, on utilise le coloriage. Généralement, un sommet est blanc s'il n'a pas été parcouru et est noir dans le cas contraire. Certains mettent les sommets à parcourir en gris mais cela n'a aucun intérêt pour le fonctionnement de l'algorithme, il s'agit juste d'un moyen pour visualiser le parcours.

Au tout début de l'algorithme, aucun sommet n'a été visité, il nous faudra donc une fonction d'initialisation qui va mettre tous nos sommets en blanc dès le début. L'algorithme d'initialisation sera donc le suivant :

Pour tous les sommets S du graphe faire
     S.couleur = blanc;

Rien de très compliqué de cette manière formelle, néanmoins, nous verrons un peu plus loin comment réaliser cela via des listes d'adjacence. Concentrons-nous plutôt pour l'instant sur l'algorithme.

Comme nous l'avons dis, pour parcourir le graphe, nous allons nous servir d'une file qui va stocker la liste des sommets à parcourir. Il faut donc commencer dans notre algorithme par y stoquer le sommet par lequel on va commencer le parcours.

Ensuite l'algorithme est relativement simple, on prend le sommet de la file et on y effectue les choses suivantes :

• - parcourir la liste des successeurs Si de S :
• - Si Si est blanc alors Si devient noir et on ajoute Si à la File.

L'algorithme s'arrête donc tout naturellement lorsque la file devient vide. Ceci veut tout simplement dire qu'il n'y a plus de sommet à visiter.

Voici donc l'algorithme :

ParcoursLargeur(G : Graphe , S : Sommet )
{
     F : File de sommets;

     Initialiser(G);

     S.couleur = Noir;
     Ajouter S à F;

     tant que F n'est pas vide faire
     
          S = Defiler(F);

          pour tous les successeurs Si de S faire

               si Si.couleur == Blanc alors
                    Si.couleur <- Noir;
                    Ajouter Si à F;
               fin si

          fin pour
     fin tant que
}

Voici donc notre premier algorithme de parcours de graphe, ce dernier est l'algorithme le plus simple que l'on peut faire avec un graphe. Il est néanmoins utilisé, tel quel ou sous une forme légèrement modifiée, dans d'autres algorithmes plus évolués. Il convient donc que vous le maîtrisiez avant de vous lancer dans d'autres algorithmes sur les graphes.

Le parcours en profondeur est le deuxième type de parcours de graphes que nous verrons ici. Il s'agit d'un parcours où l'on explore un chemin jusqu'a ce que l'on ne puisse plus avancer dans le graphe. Ce cas arrive lorsque l'on a soit parcouru tout le graphe, soit lorsque l'on est arrivé sur un sommet qui n'a pas de successeurs. Dans ce cas, il faut rebrousser chemin dans notre exploration et partir d'un sommet qui n'a pas été visité.

Nous allons donner, dans un premier temps un algorithme récursif pour le parcours en profondeur, celui ci est assez simple. En effet, il se base sur les principes suivants : si un sommet n'a pas été visité alors il faut le parcourir en profondeur. S'il a déjà été visité alors il ne faut rien faire. L'exploration récursive s'arrête tout simplement lorsque l'on a parcouru tous les sommets.

Il est très simple de montrer que l'algorithme se termine puisque le graphe a un nombre fini de sommets et qu'à chaque exploration dans le graphe, on diminue le nombre de sommets qui n'ont pas encore été visités.

Le parcours consiste donc à marquer le sommet courrant puis pour tous les sommets Si successeurs de faire un parcours en profondeur si le sommet n'a pas été marqué.

Voici donc l'algorithme récursif pour parcourir un graphe en profondeur :

Initialiser(G);

ParcoursProfondeur( Graphe G, Sommet S)
{
	S.couleur <- Noir;
	
	Pour tous les successeurs Si de S faire
		Si Si.couleur == Blanc alors
			ParcoursProfondeur(G,Si);
		Fin si
	Fin Pour		
}

Comme pour l'autre algorithme, vous avez remarquez que l'on fait appel à la fonction Initialiser avant d'appeler l'algorithme en lui même.

Voilà donc deux algorithmes très simples pour le parcours de graphes. Nous verrons dans la suite qu'ils sont utilisés assez fréquemment directement ou en impliquant de petits changements pour réaliser des algorithmes plus évolués.